extreme values can misleadingly improve R squared

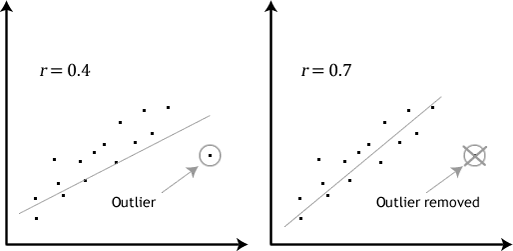
• R squared dependency on sample’s mean makes it susceptible to extreme values (e.g. outliers) when measuring for linear regression or correlation

  • This is because Pearson’s R measure distances of data points from its x-mean and y-mean – linearity and homoscedasticity assumption is critical
  • 
  • Formula to find the Pearson correlation coefficient, denoted as R
    • \[R_{xy}=\frac {\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})} { \sqrt{\sum\limits_{i=i}^{n}(x_i-\bar{x})^2 } \sqrt{\sum\limits_{i=i}^{n}(y_i-\bar{y})^2 } }\]
  • In the case where you do have outliers, the resultant R including them may mislead by either reducing the strength (when the outlier is off tangent), or improve it greatly (when outlier within the line but far off)
    • 

References

• Pearson Correlation Coefficient - Statology
• Pearson Coefficient of Correlation Explained / by Joseph Magiya / Towards Data Science

Metadata

• topic:: 00 Statistics00 Statistics
  #MOC / Hub for notes related to general statistical knowledge
  
• updated:: 2022-09-10 Private or Broken Links
  The page you're looking for is either not available or private!
  
• reviewed:: 2022-09-10 Private or Broken Links
  The page you're looking for is either not available or private!
  
• #PermanentNote